Prim 알고리즘

프림 알고리즘(Prim's Algorithm)이란?

최소 신장 트리(Minimum Spanning Tree) 구현에 사용되는 알고리즘으로 시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장하는 기법이다.

 

---

프림 알고리즘의 동작

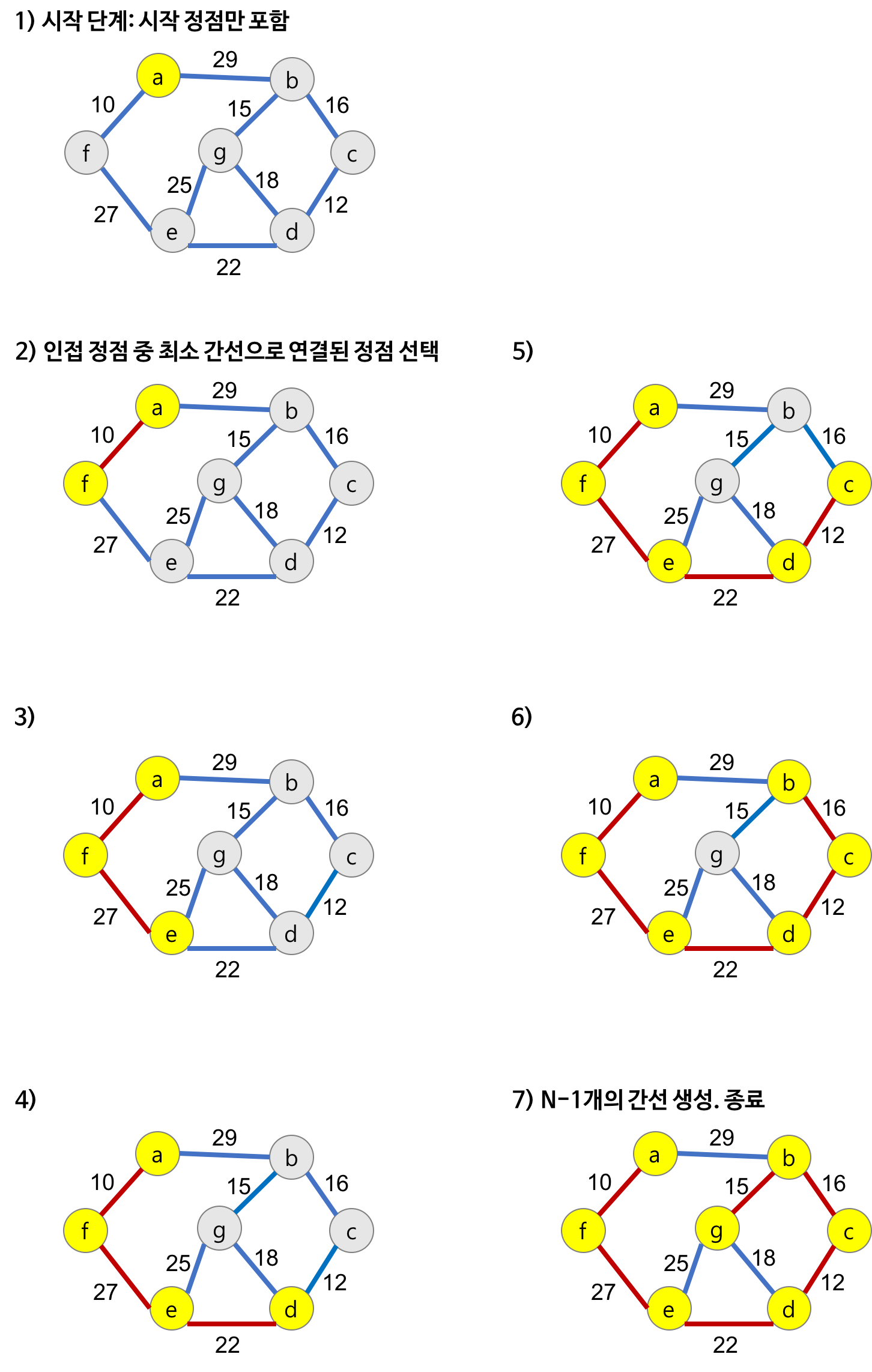
프림 알고리즘은 매 순간 최선의 조건을 선택하는 그리디 알고리즘을 바탕에 둔다. 즉, 탐색 정점에 대해 연결된 인접 정점들 중 비용이 가장 적은 간선으로 연결된 정점을 선택한다.

1. 시작 단계는 시작 노드만이 MST 집합에 속한다.
2. 트리 집합에 속한 정점들과 인접한 정점들 중 가장 낮은 가중치의 간선과 연결된 정점에 대해 간선과 정점을 MST 트리 집합에 넣는다. (사이클을 막기 위해 연결된 정점이 이미 트리가 속한다면 그 다음 순서를 넣는다.)
3. 2번 과정을 MST 집합의 원소 개수가 그래프의 정점의 개수가 될 때까지 반복한다. (간선의 가중치를 더해서 최소 신장 트리 비용 산출)

---

프림 알고리즘 시간복잡도

 모든 노드에 대해 탐색을 진행하므로 O(V)이다. 그리고 우선순위 큐를 사용하여 매 노드마다 최소 간선을 찾는 시간은 O(log V)이다. 따라서 탐색과정에는 O(V log V)가 소요된다.

그리고 각 노드의 인접 간선을 찾는 시간은 모든 노드의 차수와 같으므로 O(∑V=1degree(v))=O(2E)=O(E)다. 그리고 각 간선에 대해 힙에 넣는 과정이 O(log V)가 되어 우선순위 큐 구성에 O(Elog V)가 소요된다.

 

따라서, O(Vlog V+Elog V)로 O(Elog V)가 되겠다.(∵ E가 일반적으로 V보다 크기 때문)

 

 만약 우선순위 큐가 아니라 배열로 구현한다면 각 정점에 최소 간선을 갖는 정점 탐색을 매번 정점마다 수행하므로 O(|V|2)가 되고 탐색 결과를 기반으로 각 정점의 최소 비용 연결 정점 탐색에는 O(1)이 소요된다. 따라서 시간복잡도는 O(V2)이다.